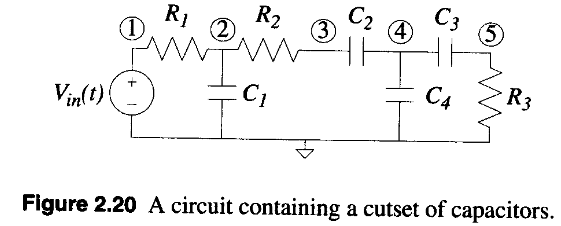
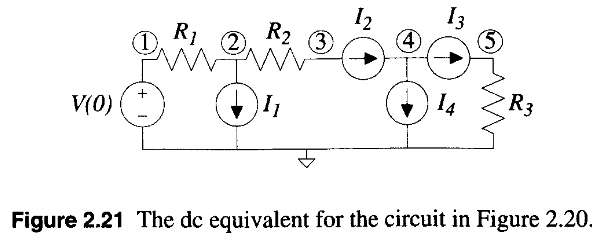
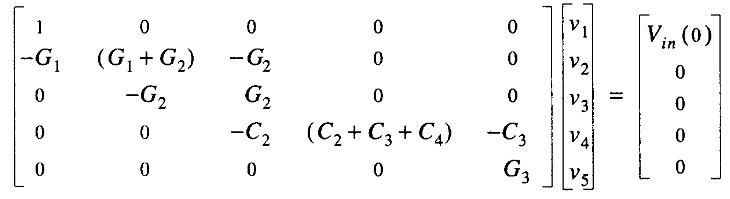In this post, the detail of linear DC nodal analysis is discussed. The material is from Book: Electronic Circuit and System Simulation Methods. Most of the content are from chapter 2 in the book.
Linear DC Nodal Analysis
For the linear DC nodal analysis perspective, the circuits can have different components:
- Resistor
- Independent voltage source
- Independent current source
- Voltage-controlled current source
- Current-controlled current source
- Voltage-controlled voltage source
- Current-controlled current source
We have seen that nodal analysis can easily deal with resistor and independent current source. Now we will see how to deal with the others.
We start from the nodal equations with only resistors and independent current sources. If there are \(N+1\) nodes, we can write down \(N+1\) equations
\[YV=I\]The equations will be indefinite. We can make it definite by picking any of the node as ground reference, then the corresponding row and column can be removed in \(Y\), such that the equations are definite. However, in this post, we will keep the original \(N+1\) equtions in the form, for the symmetry of the equations.
Matrix Stamps
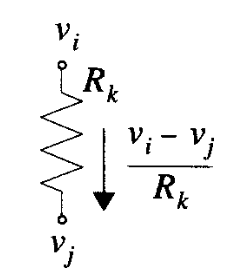
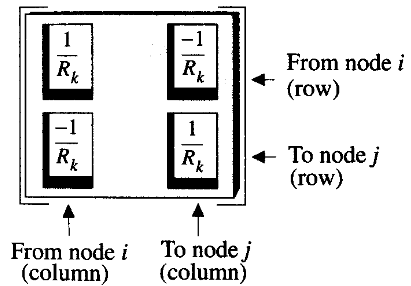
Resistor
For a resistor connecting from node \(i\) to node \(j\), it will give the matrix stamps in \(Y\) matrix.
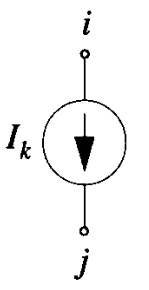
Independent Current Source
For a independent current source connecting from node \(i\) to node \(j\), it will give the matrix stamps in current vector
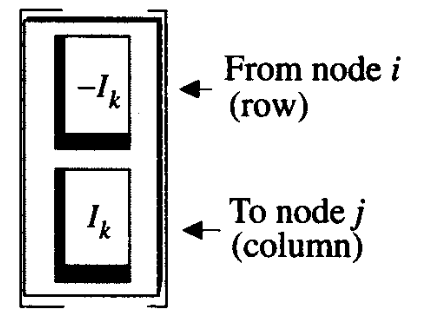
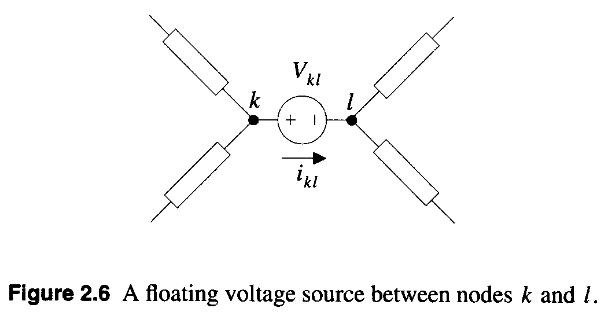
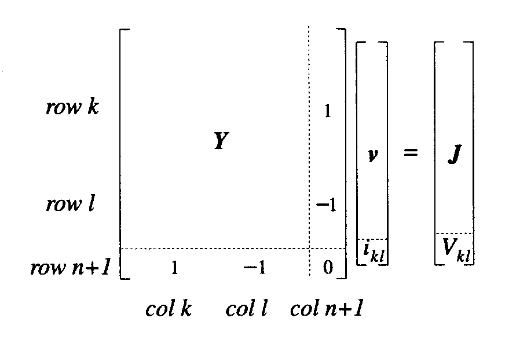
Independent Voltage Sources
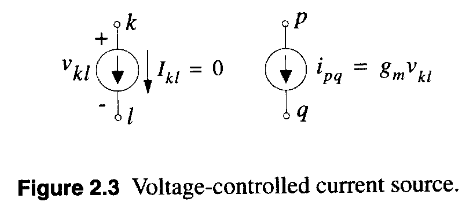
Voltage-Controlled Current Source
Voltage-controlled current source is a four-terminal element. It will give matrix stamp in \(Y\) matrix.
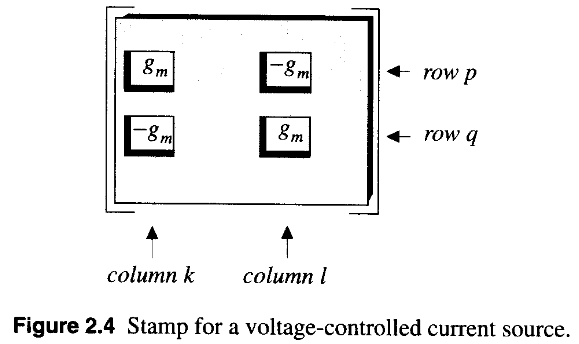
Current-Controlled Current Source
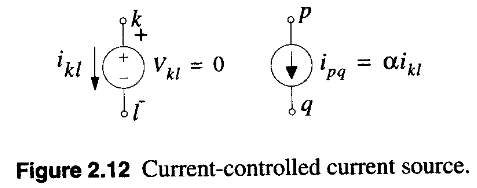
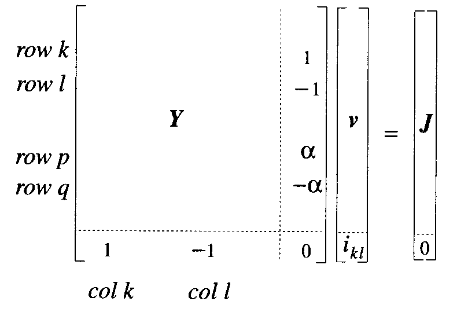
Voltage-Controlled Voltage Source
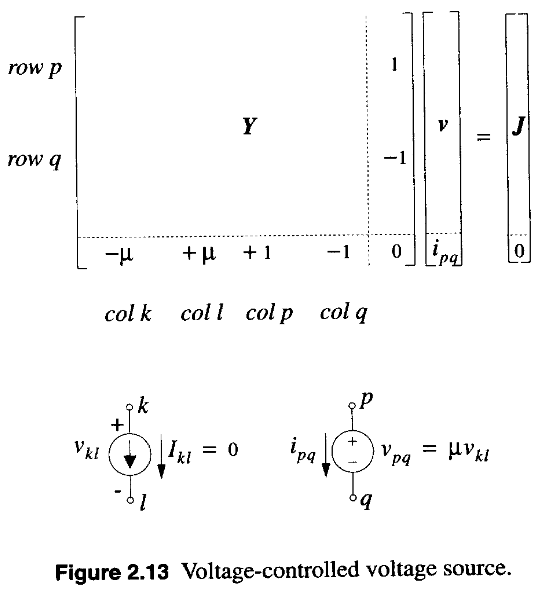
Current-Controlled Voltage Source
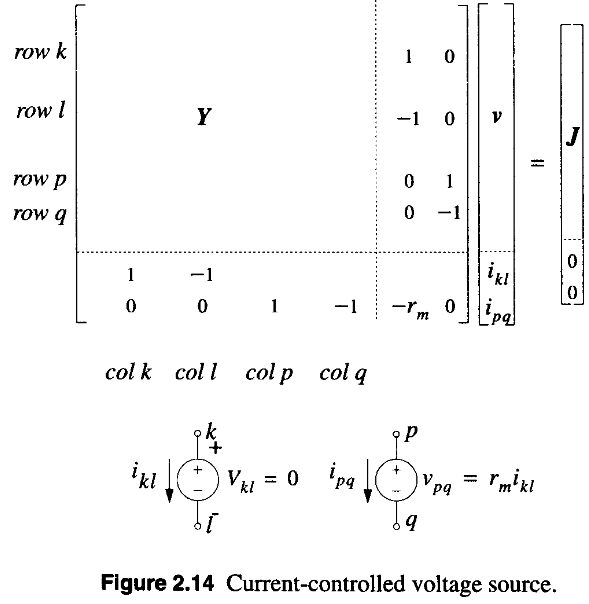
When Do Nodal Equations Fail?


DC Solution of Circuits with Energy Storage