Discrete Time Signals

\[H(s) = \mathrm{tf(a,b)} = \dfrac{a_0 s^m + a_1 s^{m-1} + \dots + a_m}{b_0 s^n + b_1 s^{n-1} + \dots + b_n}\] \[H(z) = \mathrm{tf(a,b,T_s)} = \dfrac{a_0 z^m + a_1 z^{m-1} + \dots + a_m}{b_0 z^n + b_1 z^{n-1} + \dots + z_n}\]

All the signals has sampling rate \(F_s\)

The white noise with zero mean and \(\sigma^2\) variance, it has PSD

\[S(f) = \dfrac{\sigma^2}{F_s / 2}\]

Discrete-Time Integration

\[\dfrac{1}{s} \approx T_s \cdot \dfrac{z^{-1}}{1-z^{-1}} = \dfrac{T_s}{z - 1}\] \[\dfrac{1}{1-z^{-1}} \approx \dfrac{F_s}{s}\] \[\bigg\vert \dfrac{1}{1-e^{-j2\pi f / F_s}} \bigg\vert^2 \approx \bigg\vert \dfrac{1}{2\pi f / F_s} \bigg\vert^2\]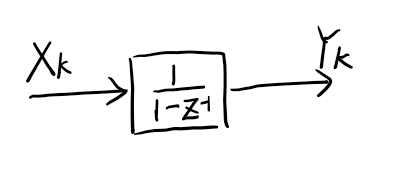

\[Y_k = Y_{k-1} + X_k, \quad \forall k \ge 1\]

and

\[Y_0 = X_0\]

\[\begin{align} Y_{k-1} &= Y_{k-2} + X_{k-1}\\ A_k &= Y_{k-1}\\ A_{k-1} &= Y_{k-2} \end{align}\]

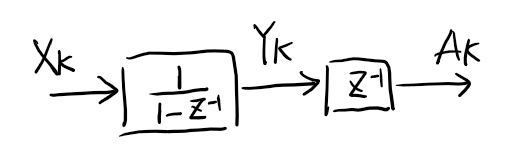
thus

\[A_{k} = A_{k-1} + X_{k-1}, \quad \forall k \ge 1\]

and

\[A_0 = 0\]