Resistance Calculation

From Lectures by Prof. Ali Hajimiri.

Example 01

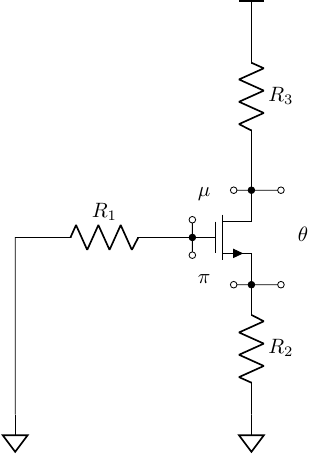Example 01

Solution

\[\begin{align} R_{\pi} &= \frac{R_1 + R_2}{1+g_m R_2}\\ R_{\mu} &= R_1 + R_3 + G_m R_1 R_3\\ G_m &= \frac{g_m}{1+g_m R_2}\\ R_{\theta} &= \frac{R_2 + R_3}{1+g_m R_2} \end{align}\]

Step-by-Step Solution

The resistance looking into the port \(\pi\)

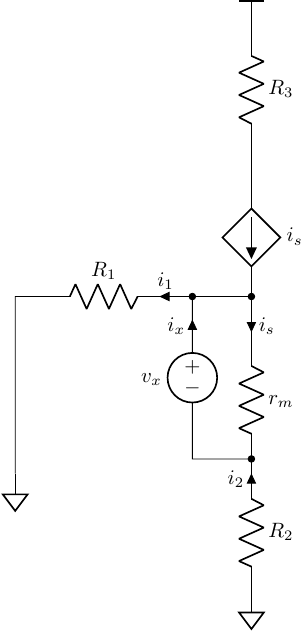The resistance looking into the port \(\pi\)

KCL

\[\begin{align} i_1 &= i_x\\ i_2 + i_s = i_x \quad \implies i_2 &= i_x - i_s = i_x - \frac{v_x}{r_m} \end{align}\]

KVL

\[\begin{align} i_1 R_1 + i_2 R_2 = v_x \end{align}\]

thus

\[\begin{align} R_{\pi} &= \frac{v_x}{i_x} = \frac{R_1 + R_2}{1+g_m R_2} \end{align}\]

The resistance looking into the port \(\mu\)

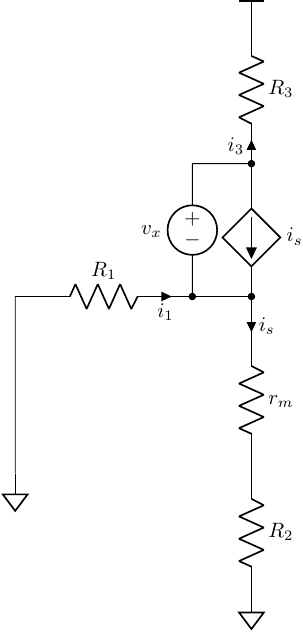The resistance looking into the port \(\mu\)

using

\[\begin{align} i_1 &= i_x\\ i_s (r_m + R_2) &= - i_1 R_1\\ i_3 + i_s &= i_x\\ v_x &= R_1 i_1 + R_3 i_3 \end{align}\]

we got

\[\begin{align} R_{\mu} &= R_1 + R_3 + G_m R_1 R_3\\ G_m &= \frac{g_m}{1+g_m R_2} \end{align}\]

The resistance looking into the port \(\theta\)

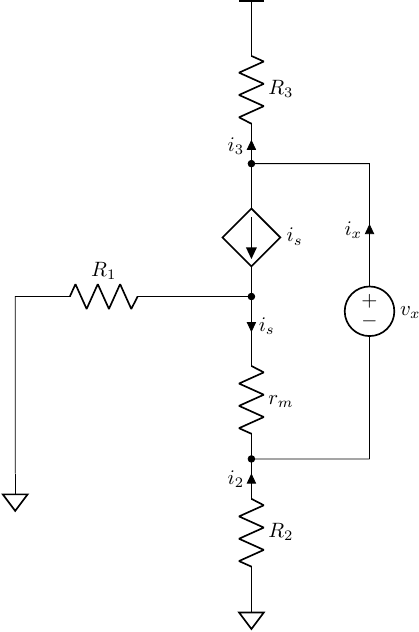The resistance looking into the port \(\theta\)

using

\[\begin{align} r_m i_s &= R_2 i_2\\ i_2 + i_s &= i_x\\ i_3 + i_s &= i_x\\ i_3 R_3 + i_2 R_2 &= v_x \end{align}\]

we got

\[R_{\theta} = \frac{R_2 + R_3}{1+g_m R_2}\]

Example 02

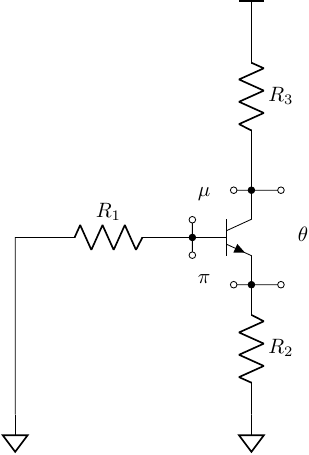Example 02

Solution

\[\begin{align} R_{\pi} &= r_{\pi} \Vert \frac{R_1 + R_2}{1+g_m R_2}\\ R_{\mu} &= R_{left} + R_{right} + G_m R_{left} R_{right}\\ R_{left} &= R_1 \Vert [r_{\pi} + (1+\beta) R_2]\\ R_{right} &= R_3\\ G_{m} &= \frac{g_m}{1 + g_m R_2}\\ R_{\theta} &= \frac{R_2 + R_3}{1+\frac{1+\beta}{\beta+g_m R_1} g_m R_2} \approx \frac{R_2 + R_3}{1 + g_m R_2} \end{align}\]