From Reza Navid’s Paper
Analytical Formulation of Phase Noise
Time-Domain Phase Noise Analysis for Switching-Based Oscillators
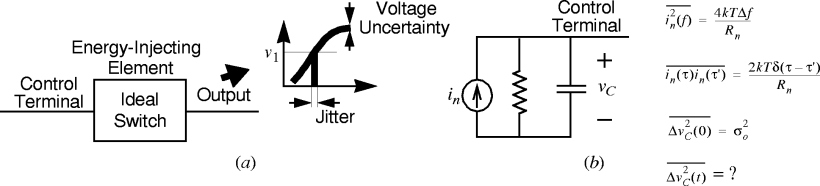
The transfer function from \(I_{n}(s)\) to \(V_c(s)\) is
\[\dfrac{V_c(s)}{I_n(s)} = R \,\Vert\, \dfrac{1}{sC} = \dfrac{\dfrac{1}{C}}{s + \dfrac{1}{RC}}\]it has a impulse response
\[v_c(t) = \dfrac{1}{C}\cdot e^{-t/RC}\]for an initial condition \(v_c(0)\), the output will be
\[v_c(0) e^{-t/RC}\]then for any input \(i_n(t)\)
\[v_c(t) = \int_{0}^{t} i_n(\tau) \cdot \dfrac{1}{C} \cdot e^{-(t-\tau)/RC} d\tau + v_c(0) e^{-t/RC}\]Since \(i_n\) is a Gaussian process with zero mean, this indicates that \(v_c\) is also a Gaussian process with zero mean. (TODO: why? see book_stochastic_differential_equations.)
Then it can be used to calculate \(\overline{v_c^2(t)}\) and also \(\overline{\Delta T_o^2}\)
Once the period jitter is calculated, phase noise can easily be calculated. In most cases (including relaxation oscillators) the output of the switching oscillators can be approximated by a stochastic square wave signal with mutually independent, Gaussian-distribution period jitter. As presented in book_topics_in_the_theory_of_random_noise_vol_2 (page 160) and also this paper, the phase noise of such a signal has a nearly Lorentzian shape around each harmonic. The phase noise around the first harmonic at an offset frequency of \(\Delta f\) is given by
\[\mathcal{L}(\Delta f) = \dfrac{f_o^3 \overline{(\Delta T_o)^2}}{(\pi f_o^3 \overline{(\Delta T_o)^2})^2 + (\Delta f)^2}\]where \(f_o\) and \(\Delta f\) are center frequency and offset frequency, respectively, and \(\overline{(\Delta T_o)^2}\) is the variance of the period.