From Xiang Gao’s Paper
Low Noise Phase Detection
Classical Three-Stage PFD/CP
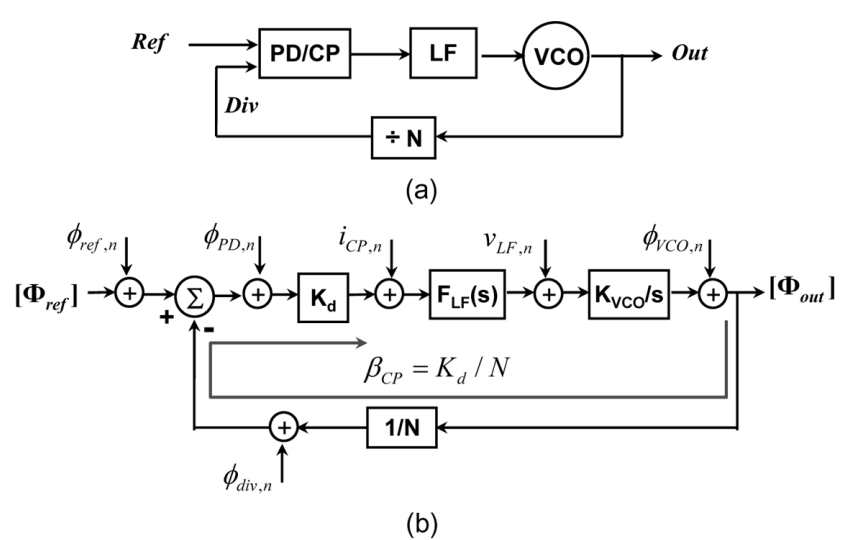
The in-band phase noise caused by CP can be calculated as
\[\begin{align} H_{CP}(s) &= \dfrac{\phi_{out,n}}{i_{CP,n}} = \dfrac{1}{\beta_{CP}} \cdot \dfrac{\beta_{CP}\cdot F_{LF}(s)\cdot\dfrac{K_{VCO}}{s}}{1 + \beta_{CP}\cdot F_{LF}(s)\cdot\dfrac{K_{VCO}}{s}}\\ &= \dfrac{1}{\beta_{CP}} \cdot \dfrac{G(s)}{1+G(s)} \end{align}\]where \(G(s)\) is the PLL open loop transfer function.
\[\mathcal{L}_{in-band,CP} \approx \dfrac{1}{2} \cdot S_{iCP,n} \cdot |H_{CP}(s)|^2 \approx \dfrac{S_{iCP,n}}{2 \beta_{CP}^2}\]for classical three-stage PFD/CP
\[\begin{align} \beta_{CP} &= \dfrac{I_{CP}}{2\pi} \cdot \dfrac{1}{N}\\ S_{iCP,n} &= 8kT\gamma \cdot g_m \cdot \dfrac{\tau_{PFD}}{T_{ref}} \end{align}\]Proposed Sub-Sampling PD/CP
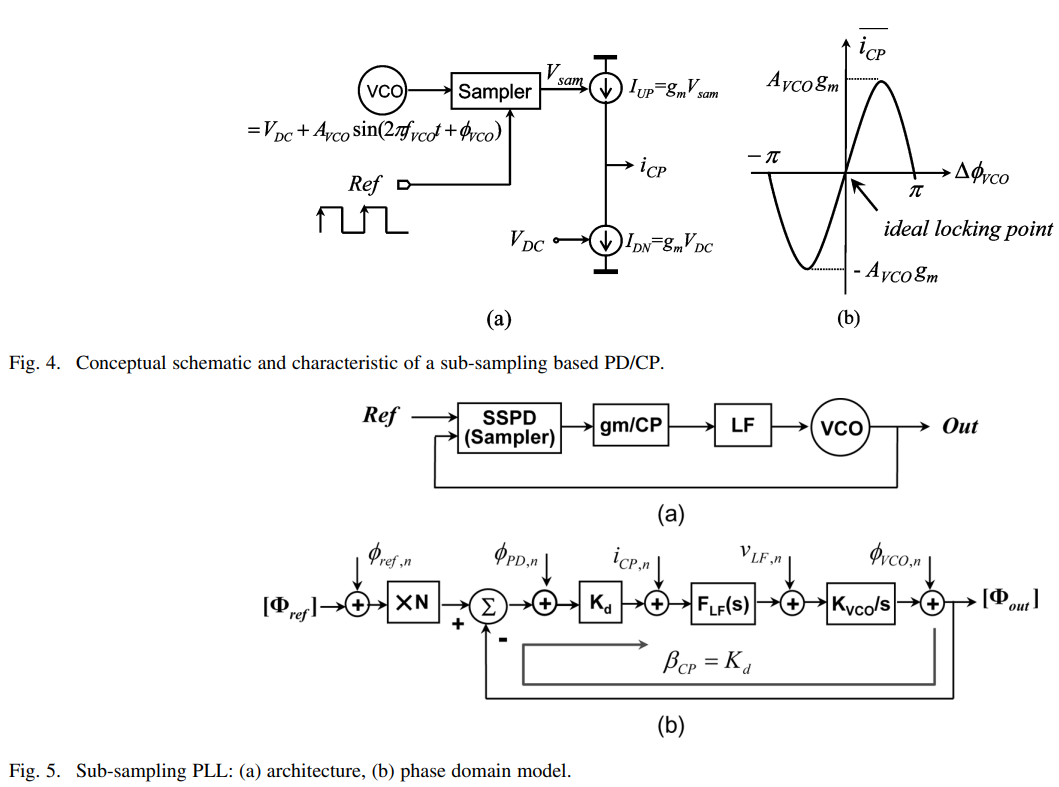
still
\[\begin{align} H_{CP}(s) &= \dfrac{\phi_{out,n}}{i_{CP,n}} = \dfrac{1}{\beta_{CP}} \cdot \dfrac{\beta_{CP}\cdot F_{LF}(s)\cdot\dfrac{K_{VCO}}{s}}{1 + \beta_{CP}\cdot F_{LF}(s)\cdot\dfrac{K_{VCO}}{s}}\\ &= \dfrac{1}{\beta_{CP}} \cdot \dfrac{G(s)}{1+G(s)} \end{align}\]but for sub-sampling PD/CP
\[\begin{align} \beta_{CP} &= A_{VCO} \cdot g_m\\ S_{iCP,n} &= 8kT\gamma \cdot g_m \end{align}\]