PLL Study

Inductor Simulation

using sp or psp simulation to simulate inductor, we calculate the Z parameter

\[\begin{bmatrix} V_1\\ V_2 \end{bmatrix}= \begin{bmatrix} Z_{11} & Z_{12} \\ Z_{21} & Z_{22} \end{bmatrix} \begin{bmatrix} i_1\\ -i_1 \end{bmatrix}\] \[Z_{diff} = \dfrac{V_1-V_2}{i_1} = Z_{11} + Z_{22} - Z_{12} - Z_{21}\] \[L_s = \dfrac{\text{Im}(Z_{diff})}{2\pi f}\] \[R_s = \text{Re}(Z_{diff})\] \[Q = \dfrac{\text{Im}(Z_{diff})}{\text{Re}(Z_{diff})}\] \[R_p = (1+Q^2)R_s\]

In virtuoso

Imagz = imag(zpm('psp 1 1)) + imag(zpm('psp 2 2)) - imag(zpm('psp 1 2)) - imag(zpm('psp 2 1))
Ls = Imagz / 2 / 3.14 / xval(Imagz)
Rs = real(zpm('psp 1 1)) + real(zpm('psp 2 2)) - real(zpm('psp 1 2)) - real(zpm('psp 2 1))
Q = Imagz / Rs
Rp = (1+Q*Q)*Rs

Capacitor Simulation

\[C_s = -\dfrac{1}{2\pi f} \cdot \dfrac{1}{Im(Z_{diff})}\] \[R_s = Re(Z_{diff})\]

Phase Noise

References:

A Charge-Sharing Locking Technique With a General Phase Noise Theory of Injection Locking

Reference phase noise

\[\begin{align} \mathcal{L}_{ref}(f) &= \dfrac{1}{2} S_{\phi} = \dfrac{1}{2} S_{t} (2\pi F_{ref})^2\\ &= \dfrac{1}{2} \cdot \dfrac{\sigma_{t}^2}{F_{ref}/2} \cdot (2\pi F_{ref})^2\\ &= 4\pi^2 F_{ref} \cdot \sigma_{t}^2 \end{align}\]

For example, \(\sigma_t = 112.5 \,\mathrm{ fs}\) with \(F_{ref} = 200\,\mathrm{ MHz}\), \(\mathcal{L}_{ref} = -160 \,\mathrm{ dBc/Hz}\).

However, this is the reference phase noise in the reference frequency domain. To the output it will be multiplied by \(N^2\) and low-passed by the loop filter.

VCO phase noise

\[\begin{align} \mathcal{L}_{osc}(f) &= \dfrac{1}{2} S_{\phi} = \dfrac{1}{2}S_t (2\pi F_{osc})^2\\ &= \dfrac{1}{2} \cdot \dfrac{\sigma_t^2}{F_{osc}/2} \cdot \left(\dfrac{F_{osc}}{2\pi f}\right)^2 \cdot (2\pi F_{osc})^2\\ &= \sigma_t^2 \cdot \dfrac{F_{osc}^3}{f^2} \end{align}\]

For example, \(\sigma_t = 1 \,\mathrm{fs}, F_{osc} = 10\,\mathrm{GHz}, f = 10\,\mathrm{MHz}\), \(\mathcal{L}_{osc}(f) = -140\,\mathrm{dBc/Hz}\).

Fractional-N PLL quantization noise:

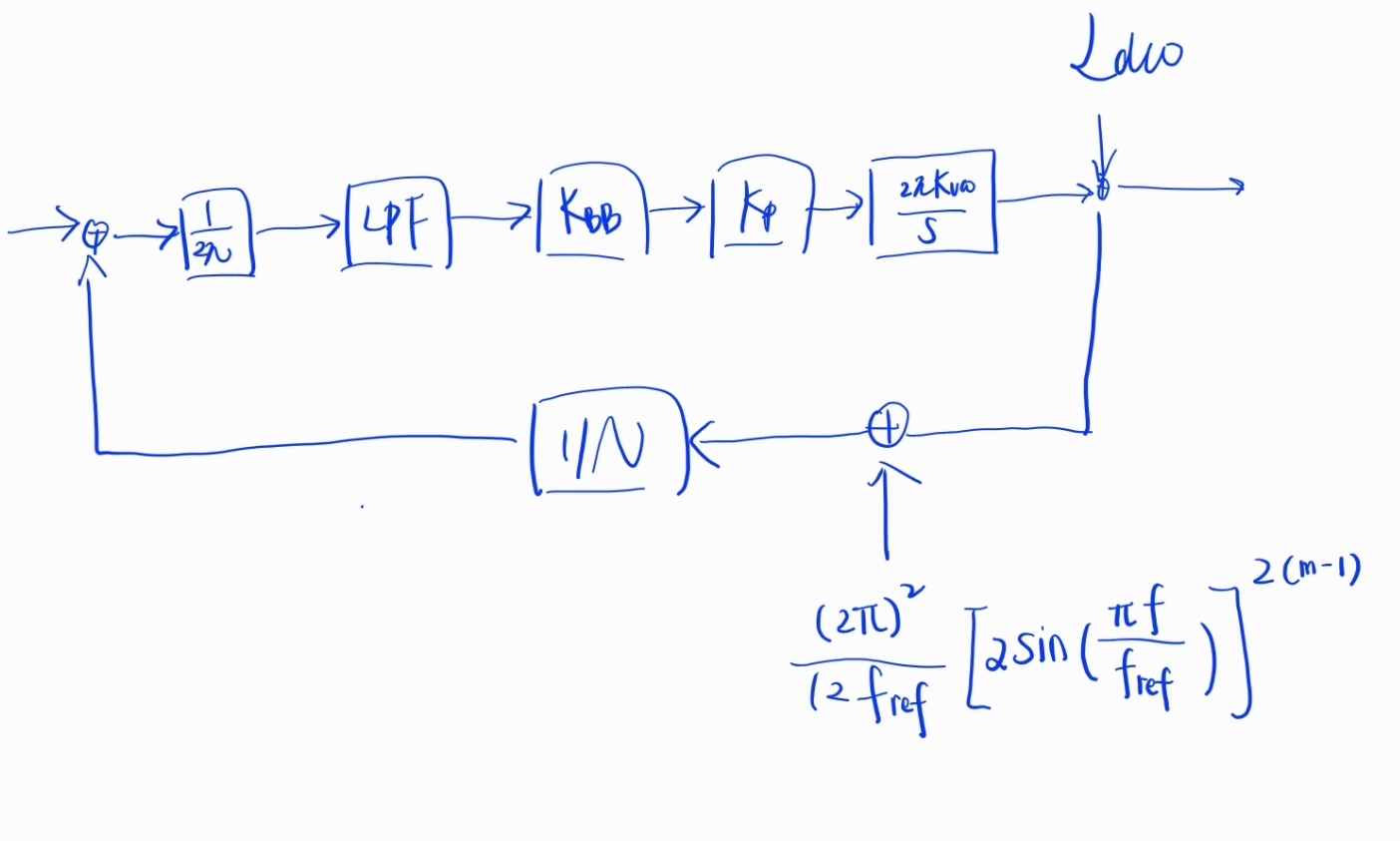
BBPLL Theory

Multirate time-domain model

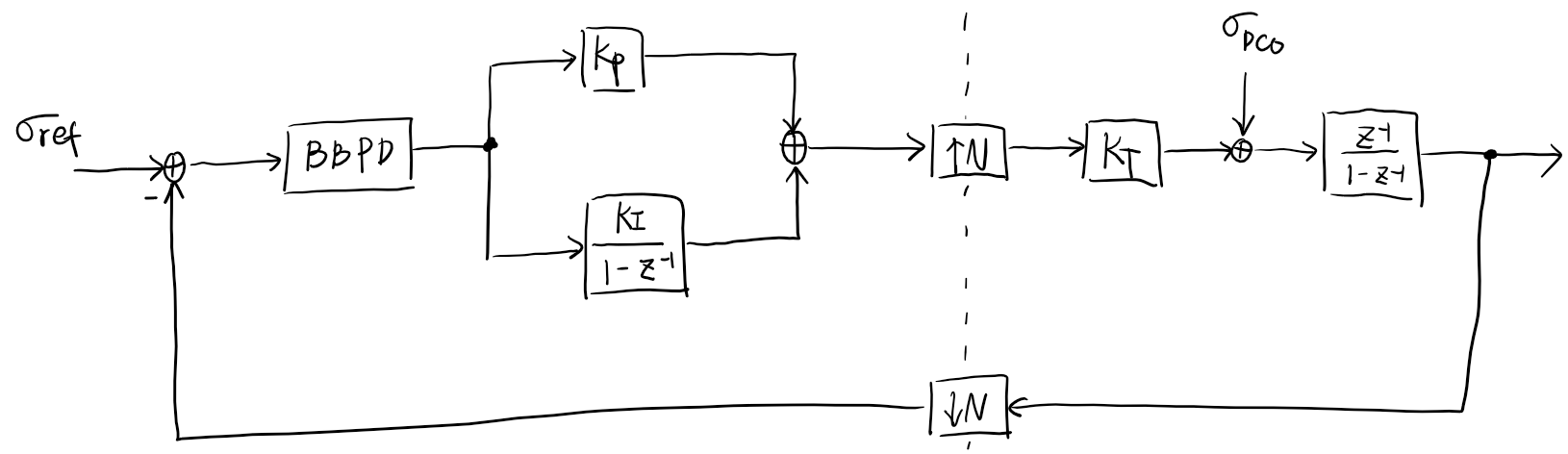
Convert to single-rate model

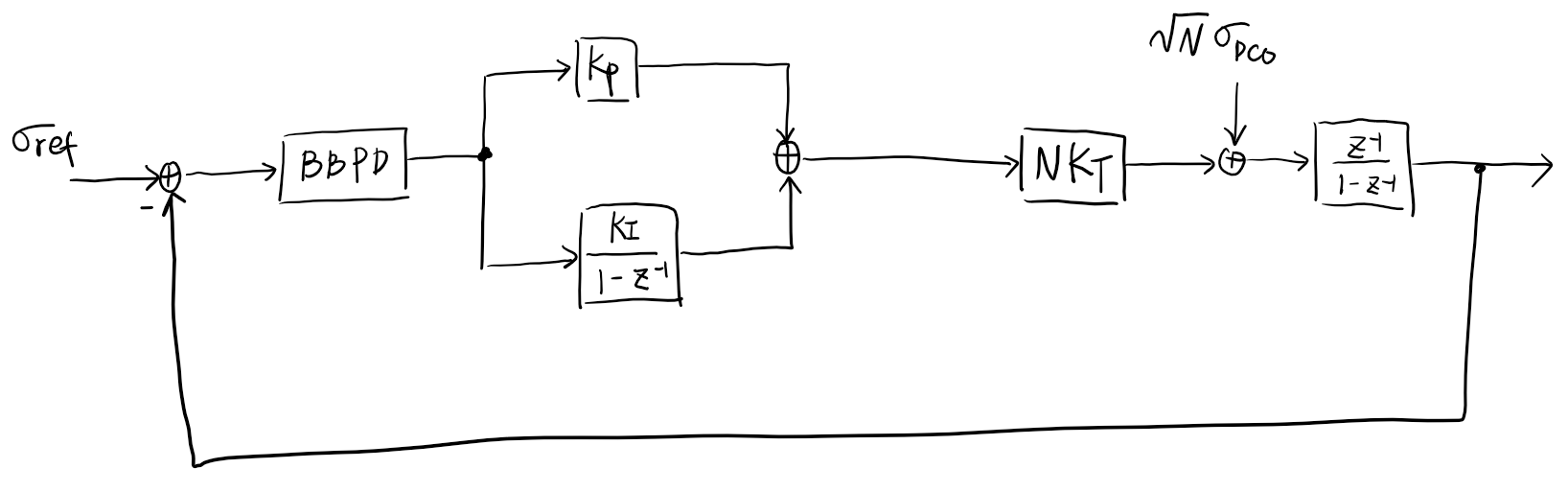
Equivalent linear model

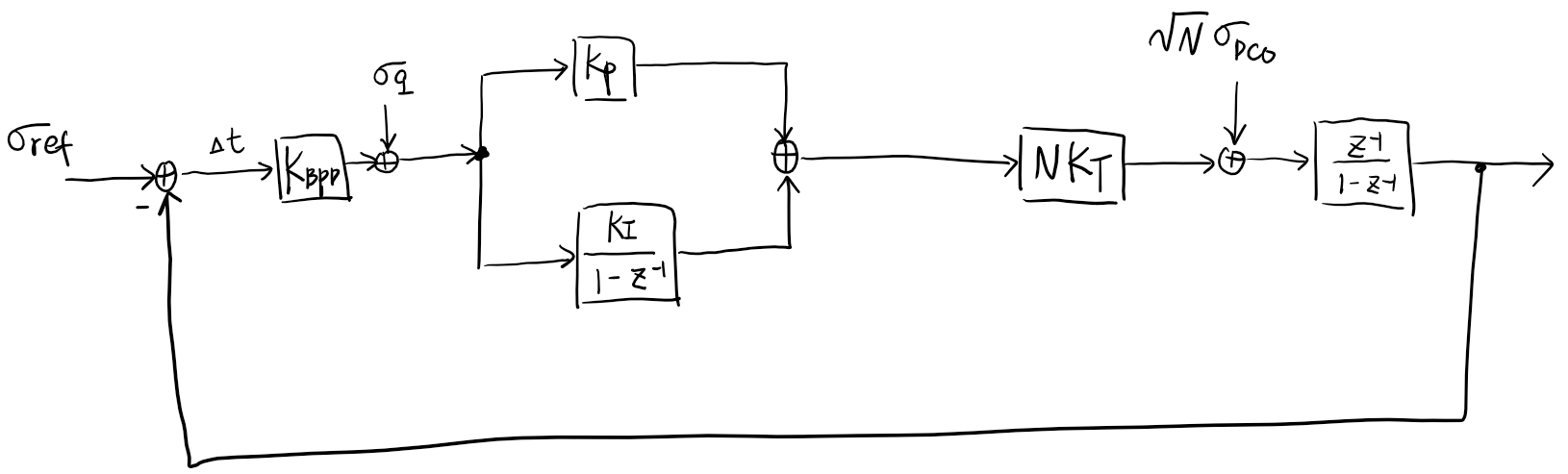
Under some assumption, approximately

\[K_{BPD} = \sqrt{\dfrac{2}{\pi}} \cdot \dfrac{1}{\sigma_{\Delta t}}\] \[\sigma_q^2 = 1 - K_{BPD}^2 \cdot \sigma_{\Delta t}^2 = 1 - \dfrac{2}{\pi}\]

Given \(\sigma_{ref}, \sigma_{DCO}, K_P, K_I, N, K_T\), we want to find the value of \(K_{BPD}\). For simplicity, we assume \(K_I\) is very small (\(K_I \ll K_P\)) such that we can ignore it. And we denote \(\chi = N K_{BPD} K_P K_T\).

\[\begin{align} Y_1[k+1] &= Y_1[k] + \chi \left(\sigma_{ref}[k] - Y_1[k]\right)\\ &= (1-\chi) Y_1[k] + \chi \sigma_{ref}[k] \end{align}\]

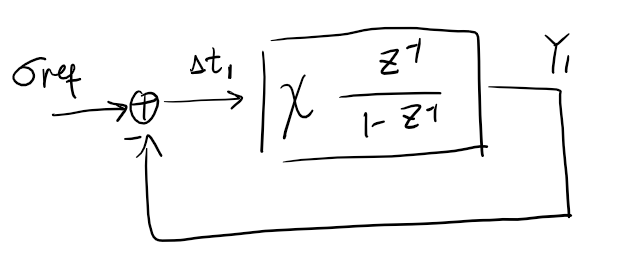
since \(Y_1[k]\) and \(\sigma_{ref}[k]\) are independent

\[\sigma_{Y_1}^2 = (1-\chi)^2 \sigma_{Y_1}^2 + \chi^2 \sigma_{ref}^2\] \[\sigma_{Y_1}^2 = \dfrac{\chi}{2-\chi} \sigma_{ref}^2\] \[\sigma_{\Delta t_1}^2 = \sigma_{ref}^2 + \sigma_{Y_1}^2 = \dfrac{2}{2-\chi} \sigma_{ref}^2\]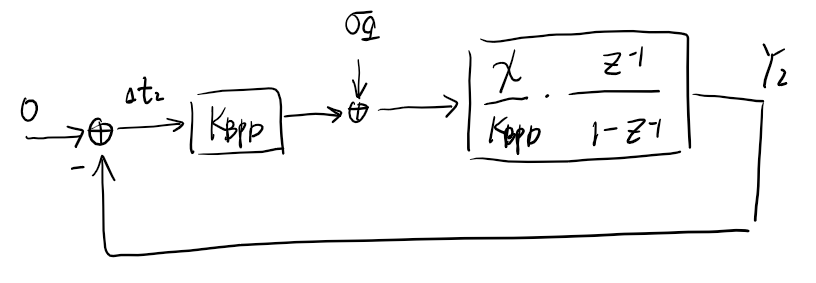

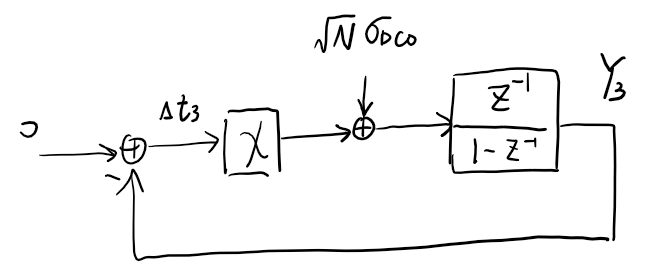
\[\begin{align} Y_2[k+1] &= Y_2[k] + \dfrac{\chi}{K_{BPD}}\left(\sigma_q[k] - K_{BPD} Y_2[k]\right)\\ &= \left(1 - \chi\right) Y_2[k] + \dfrac{\chi}{K_{BPD}} \sigma_q[k] \end{align}\] \[\sigma_{\Delta t_2}^2 = \sigma_{Y_2}^2 = \dfrac{\chi}{2-\chi} \dfrac{\sigma_{q}^2}{K_{BPD}^2}\]

\[\begin{align} Y_3[k+1] &= Y_3[k] + (\sqrt{N} \sigma_{DCO}[k] - \chi Y_3[k])\\ &= (1-\chi) Y_3[k] + \sqrt{N} \sigma_{DCO}[k] \end{align}\] \[\sigma_{\Delta t_3}^2 = \sigma_{Y_3}^2 = \dfrac{N}{\chi(2-\chi)} \sigma_{DCO}^2\] \[\begin{align} \sigma_{\Delta t}^2 &= \sigma_{\Delta t_1}^2 + \sigma_{\Delta t_2}^2 + \sigma_{\Delta t_3}^2\\ &= \dfrac{2}{2-\chi} \sigma_{ref}^2 + \dfrac{\chi}{2-\chi} \dfrac{\sigma_q^2}{K_{BPD}^2} + \dfrac{N}{\chi(2-\chi)}\sigma_{DCO}^2 \end{align}\]

combine with

\[K_{BPD} = \sqrt{\dfrac{2}{\pi}} \cdot \dfrac{1}{\sigma_{\Delta t}}\] \[\sigma_q^2 = 1 - \dfrac{2}{\pi}\]

After some algebra (please provide)

\[\sigma_{\Delta t} = \dfrac{\eta}{2} + \sqrt{\left(\dfrac{\eta}{2}\right)^2 + \sigma_{ref}^2}\] \[\eta = \sqrt{\dfrac{\pi}{2}} \cdot \left(\dfrac{\sigma_{DCO}^2}{2 K_P K_T} + \dfrac{N K_P K_T}{2}\right)\] \[K_{P,opt} = \dfrac{\sigma_{DCO}}{K_T \sqrt{N}}\] \[\eta_{opt} = \sqrt{\dfrac{N \pi}{2}} \sigma_{DCO}\] \[\Delta t[k] = \sigma_{ref}[k] - \sigma_{out}[k]\] \[\sigma_{\Delta t}^2 = \sigma_{ref}^2 + \sigma_{out}^2\] \[\sigma_{out}^2 = \sigma_{\Delta t}^2 - \sigma_{ref}^2\]

BBPLL locking time, Frequency Synthesizers Based on Fast-Locking Bang-Bang PLL for Cellular Applications

1

• JSSC 2009

Circuit Design

2

• ISSCC 2018
• JSSC 2019

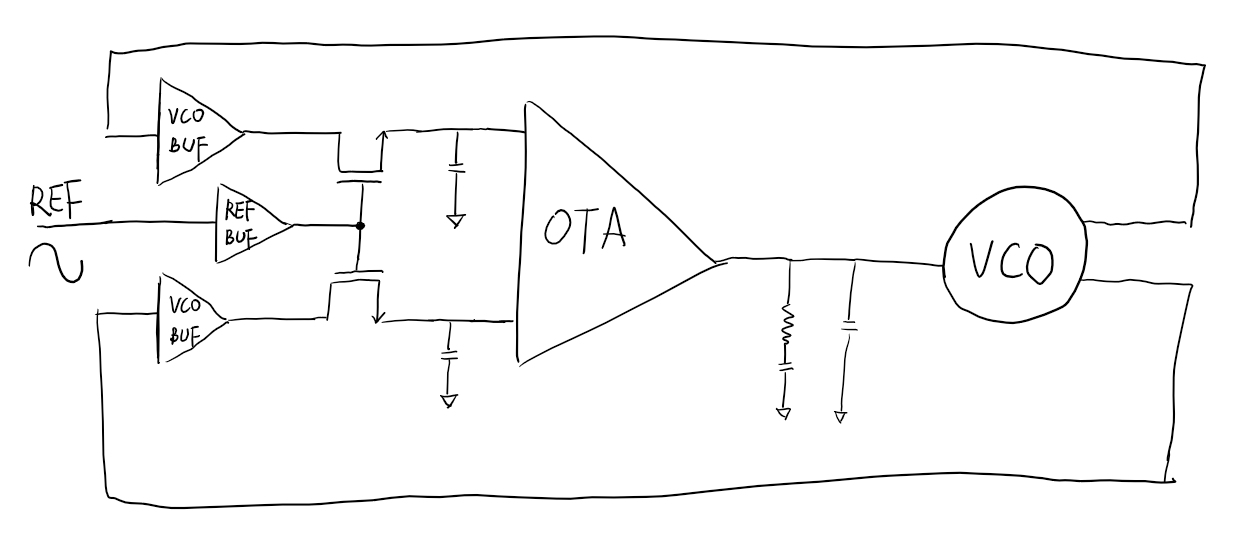
Circuit Design

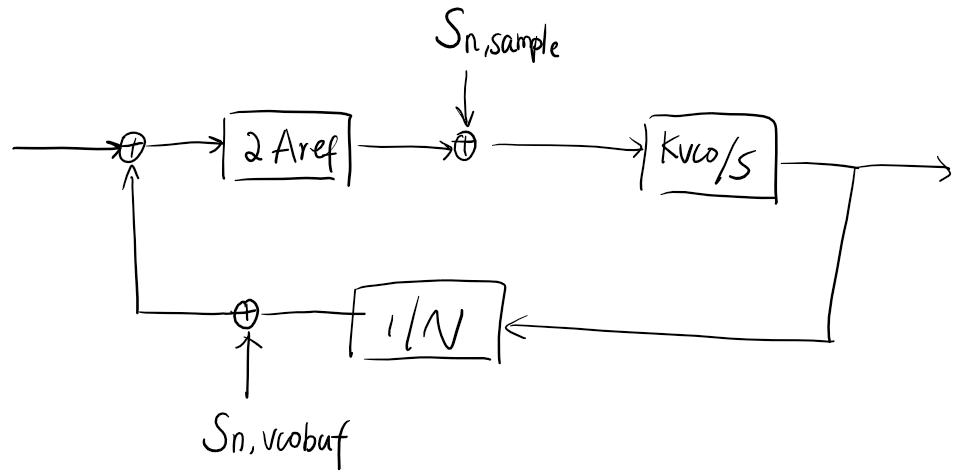
The circuits is composed of a VCO, a sampler, one reference buffer and two VCO buffer.

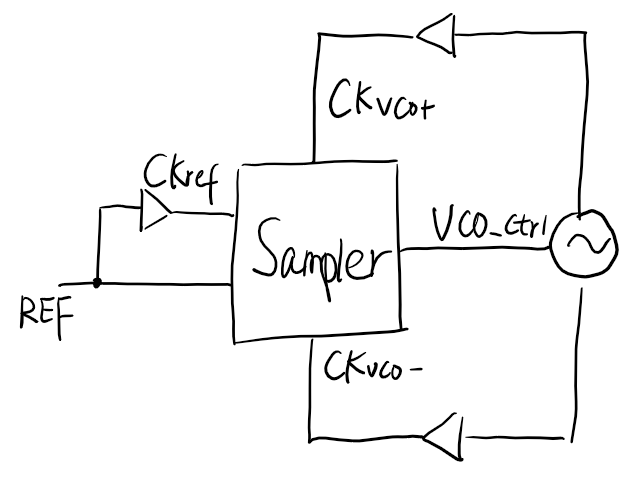
Sampler

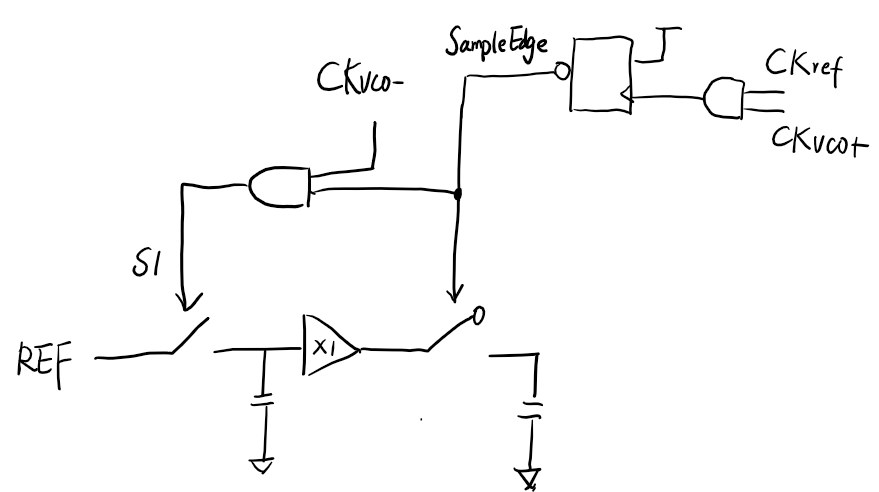
We have to make sure the SampleEdge’s falling edge comes when CKvco- is 0. There are two possibilities, one is CKref asserts when CKvco+ is 0; another one is CKref asserts when CKvco+ is 1. In either case, SampleEdge’s falling edge happens when CKvco+ is 1, then CKvco- is 0.

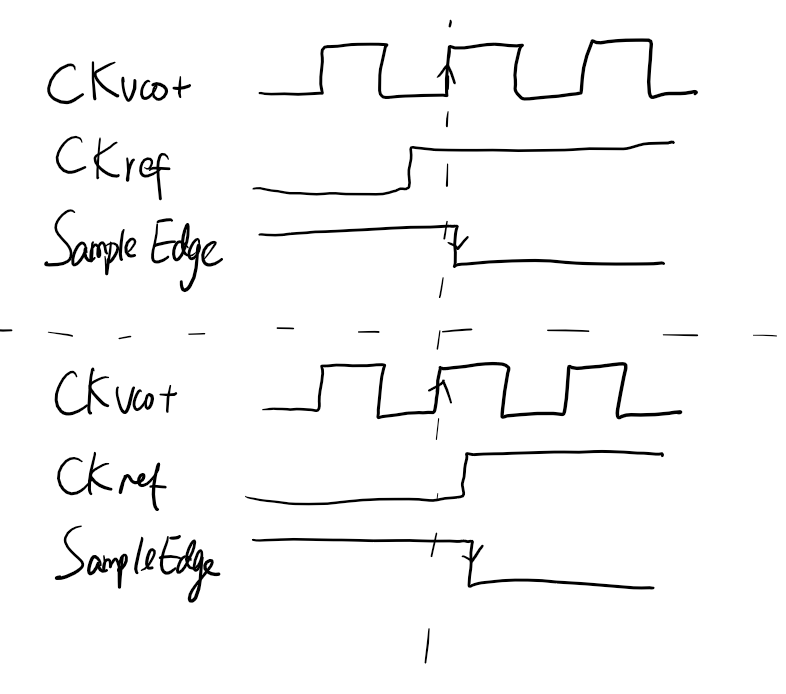
The diagram shows single-ended sampling, but the real circuits adopts differential sampling.

Reference buffer

The reference buffer is calibrated per die such that CKref transit at the crossover of the reference signal.

Inband Phase Noise Analysis

\[S_{n,sample} = \dfrac{2kT}{C_{sample}} \cdot \dfrac{1}{F_{ref}/2} = \dfrac{4kT}{C_{sample} \cdot F_{ref}}\] \[\mathcal{L}_{n,sample} = \dfrac{1}{2} \cdot S_{n,sample} \cdot \left(\dfrac{N}{2A_{ref}}\right)^2 = \dfrac{2kT}{C_{sample}\cdot F_{ref}} \cdot \left(\dfrac{N}{2A_{ref}}\right)^2\] \[S_{n,vcobuf} = \dfrac{\overline{\Delta V^2}}{SL^2} \cdot (2\pi F_{ref})^2 \cdot \dfrac{1}{F_{ref}/2}\] \[\mathcal{L}_{n,vcobuf} = \dfrac{1}{2} \cdot N^2 \cdot S_{n,vcobuf}\]