VCO 01

\[\mathcal{L}_{VCO}(f_m) = \dfrac{10^{\mathrm{FOM}_{\mathrm{VCO}}/10}}{P_{\mathrm{VCO}}/1 \mathrm{mW}} \cdot \dfrac{f_{\mathrm{VCO}}^2}{f_m^2}\]

for \(LC\) oscillator, take the simple model shown below

\[\begin{align} \mathcal{L}(\omega) &= \dfrac{4kTR}{\dfrac{1}{2}V_0^2} \bigg(\dfrac{\omega_0}{2Q\omega}\bigg)^2\\ &= \dfrac{4kT}{P_{dissipation}} \bigg( \dfrac{\omega_0}{2Q\omega} \bigg)^2 \end{align}\]

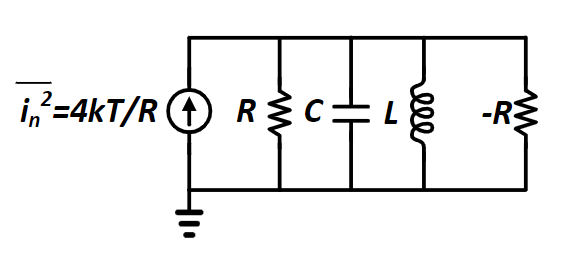
where

\[\begin{align} Q &= \dfrac{R}{\omega_0 L}\\ \omega_0 &= \dfrac{1}{\sqrt{LC}} \end{align}\]

If we use such implementation like below

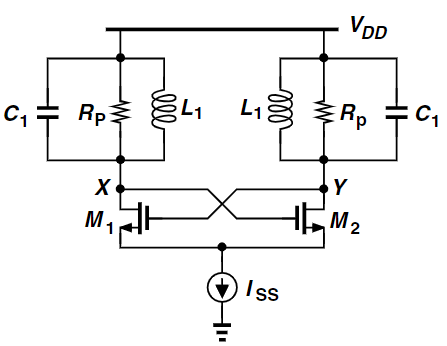
It has a peak differential output swing of

\[V_{XY} \approx \dfrac{4}{\pi} I_{ss}R_p\]

VCO Model Specification

Let’s specify \(V_0, P_{\mathrm{VCO}}, \mathrm{FOM_{VCO}}\)

\[\begin{align} P_{\mathrm{VCO}} &= \dfrac{V_0^2}{2R_p}\\ R_p &= \dfrac{V_0^2}{2 P_{\mathrm{VCO}}}\\ Q^2 &= \dfrac{kT}{1mW} \cdot 10^{-\mathrm{FOM_{VCO}}/10}\\ Q &= \sqrt{\dfrac{kT}{1mW} \cdot 10^{-\mathrm{FOM_{VCO}}/10}}\\ L_1 &= \dfrac{R_p}{2\pi f_{target} Q}\\ I_{ss} &= \dfrac{V_0}{R_p} \cdot \dfrac{\pi}{4}\\ g_m &= \dfrac{2}{R_p} = \sqrt{4 K_N \cdot \dfrac{1}{2} I_{ss}}\\ K_N &= \dfrac{2}{I_{ss} R_p^2} \end{align}\]

let the control voltage range from \(V_{cl}\) to \(V_{ch}\)

\[C_x = C_m \dfrac{V_{ch} - V_{x}}{V_{ch} - V_{cl}}\]

we can specify \(f_{min}, f_{max}\), let’s have

\[\begin{align} f_{min} &= \dfrac{1}{2\pi \sqrt{L_1 (C_1 + C_m)}}\\ f_{max} &= \dfrac{1}{2\pi\sqrt{L_1 C_1}} \end{align}\] \[\begin{align} C_1 &= \dfrac{1}{L_1 \cdot (2\pi f_{max})^2}\\ C_m &= \dfrac{1}{L_1 \cdot (2\pi f_{min})^2} - \dfrac{1}{L_1 \cdot (2\pi f_{max})^2}\\ K_{\mathrm{VCO}} &\approx \dfrac{2\pi (f_{max} - f_{min})}{V_{ch}-V_{cl}} \end{align}\]

Summary

In summary, the value we specified is

\(V_0\)

\(P_{\mathrm{VCO}}\)

\(\mathrm{FOM_{VCO}}\)

\(V_{cl}\)

\(V_{ch}\)

\(f_{min}\)

\(f_{target}\)

\(f_{max}\)

\[\begin{align} R_p &= \dfrac{V_0^2}{2 P_{\mathrm{VCO}}}\\ Q &= \sqrt{\dfrac{10^{\mathrm{FOM_{VCO}}/10}}{kT/1mW}}\\ L_1 &= \dfrac{R_p}{2\pi f_{target} Q}\\ I_{ss} &= \dfrac{V_0}{R_p} \cdot \dfrac{\pi}{4}\\ K_N &= \dfrac{2}{I_{ss} R_p^2}\\ C_1 &= \dfrac{1}{L_1 \cdot (2\pi f_{max})^2}\\ C_m &= \dfrac{1}{L_1 \cdot (2\pi f_{min})^2} - \dfrac{1}{L_1 \cdot (2\pi f_{max})^2}\\ K_{\mathrm{VCO}} &\approx \dfrac{f_{max} - f_{min}}{V_{ch}-V_{cl}} \end{align}\]